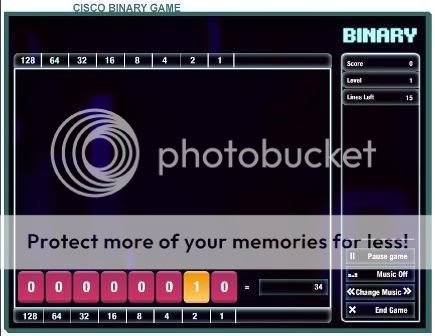
بھیا میں نے آپ سے کہا تھا نا کہ میں آپ کو بائینری سکھاؤں گی۔

تو یہ رہے گولڈن اصول ۔۔۔۔
بائینری نظام میں صرف
دو عدد ہیں ۔ صفر اور ایک
ڈیناری نظام میں دس عدد ہوتے ہیں۔ صفر۔1یک۔ دو۔ تین ۔ چار۔ پانچ ۔ چھ - سات ۔ آٹھ ۔ نو
اس لیے ڈینری نظام کا بیس 10 ہے اور
بائینری کا بیس 2
ڈینیری کی گنتی..... بائینری گنتی
100.10.1...........64.32.16.8.4.2.1..128..256.........
0 ............................
0 0 0 0
1 ............................
1 0 0 0
2 ............................
0 1 0 0
3 ............................
1 1 0 0
4 ............................0
0 1 0
5 ............................1
0 1 0
6 ............................0
1 1 0
7 ............................1
1 1 0
8.............................0 0
0 1
9 ............................1 0
0 1
0 1 ........................0 1
0 1
1 1 ........................1 1
0 1
2 1 ........................0 0
1 1
3 1 ........................1 0
1 1
4 1.........................0 1
1 1
5 1.........................1 1
1 1
بھیا میں نےکہا تھا نا کہ میں بائینری کی گنتی اربوں تک لکھ کے دکھا سکتی ہوں ۔۔۔۔
تم نے کہا تھا!!!۔۔۔

ان آپ اس
پیٹرن کودیکھیں۔
پہلے کالم کا پیٹرن
0
1
0
1
دوسرے کالم میں
0
0
1
1
تیسرے کالم کا
0
0
0
0
1
1
1
1
تو آپ اس پیٹرن کو فالو کریں اور بتائیں کہ اگلا پیٹرین کیا ہوگا۔
اوکے ۔۔۔

چوتھے کالم میں
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
بالکل صحیح ۔۔۔ آپ اسمارٹ ہیں بہت جلد کیچ کرلیتے ہیں۔
ایک بات اور
کیا ۔۔۔۔۔

جمع کرنے کے اصول
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 10
اور کچھ۔
بائینری کا بیس 2 ۔۔۔اسطرح ہوتا ہے
1...2...4...8...16...32...64...128...256.... ۔۔۔ وغیرہ
یعنی یہ سب 2 کے مرکب ہیں۔
اس کی مدد سے بڑے سے بڑا نمبر لکھ سکتے ہیں۔
سسٹر ۔۔۔

کیا پیارے بھیا۔۔۔
[/IMG]
بھیا ۔ میں چلی میرا خیال ہے کہ اس سے پہلے کےسہانہ اپنے بھائی سے غلط بائینری سیکھے۔ میں جلدی سے جاکر سہانہ کو