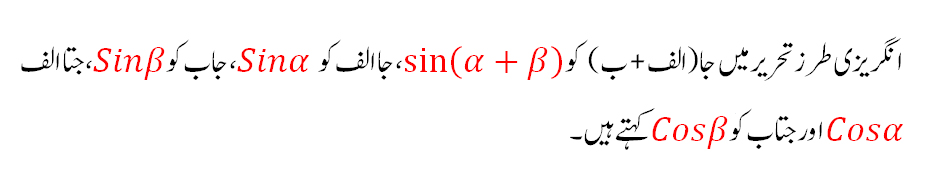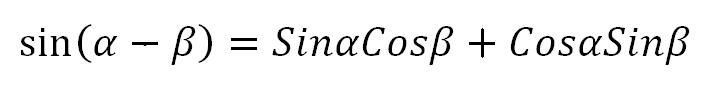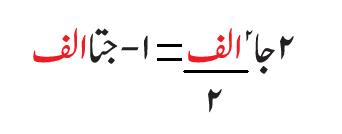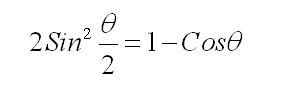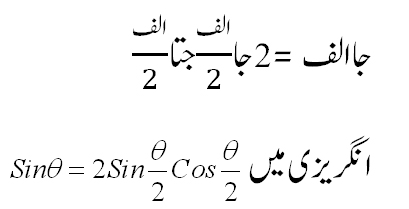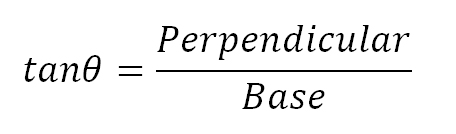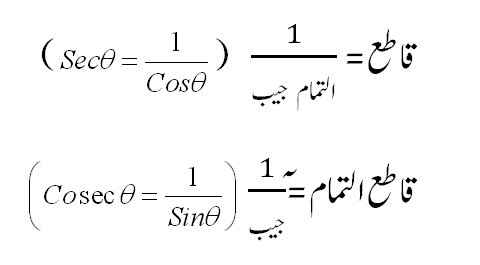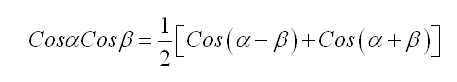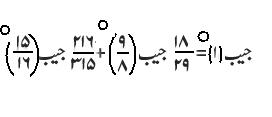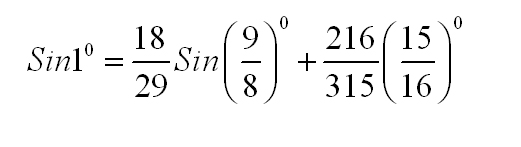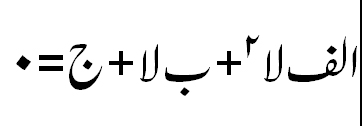حمیر یوسف
محفلین
اس لڑی میں میری کوشش ہوگی کہ دنیائے اسلام کے ان قدیم مایہ ناز سائنسدانوں کا تعارف کروایا جائے ، جنکی خدمات کے متعرف آج بھی سائینسی دنیا خصوصا مغرب حصہ کرتا ہے اور اپنی کتب میں انکا تذکرہ بہت واضح الفاظ میں کرتا ہے۔ یہ وہ سائنسدان تھے ، جنہوں نے اس وقت دنیائے اسلام میں سائنس کا جھنڈا گاڑا جب یورپ اپنی تاریکیوں میں ڈوبا ہوا تھا اور لندن و پیرس ایک تنگ و تاریک گاؤں سے زیادہ حیثیت نہیں رکھتے تھے۔ ان کے کارنامہ پڑھ کر آپ لوگوں کو اندازہ ہوگا کہ مسلم دنیا بھی سائنسی کارناموں اور تخیلات سے کبھی خالی نہیں رہی۔ جس دین کی پہلی تعلیم کا آغاز ہی "اقراء" سے ہوتا ہو، کیا وہ کبھی "اقراء" سے نابلد رہ سکتی ہے؟ اس لڑی کو مرتب کرنے کے لئے مجھے کافی ساری کتابوں کی مدد لینی پڑی ، جسکا تذکرہ میں انشاء اللہ گاہے بگاہے کرتا رہونگا۔ کافی طویل سلسلہ ہے، اس لئے ایک سے زیادہ حصوں پر مشتمل ہوگا۔جاب کی مصروفیت کی وجہ سے ٹائپنگ میں وقت کی کمی سے پوسٹنگ میں خلل آسکتا ہے، اس لئے اس سلسلے کے لئے ایڈوانس میں معذرت۔
جابر بن حیان (786 ع)
وہ کیمیا کے تمام تجرباتی عملوں مثلا حل کرنا (Dissolve) ، فلٹر کرنا (Filtrate) کشید کرنا (Distillation ) عمل تصعید (Sublimation (اشیاء کا جوہر اڑانا اور قلماؤ (Crystallization) کے ذریعےاشیاء کی قلمیں بنانا، اس سب سے وہ واقف تھا، بلکہ اپنے کیمیائی تجربوں میں ان سے بکثرت کام بھی لیتا تھا۔ اس نے اپنی کیمیا کی کتابوں میں فولاد بنانے، چمڑے کو رنگنے، دھاتوں کو مصفی کرنے (Metallurgy) موم جامہ بنانے، لوہےکو زنگ سے بچانے کےک لئے اس پر وارنش کرنے، بالوں کو سیاہ کرنے کے لئے خضاب تیار کرنے اور اس قسم کی بیسوں مفید اشیاء بنانے کے طریقے بیان کیئے ہیں۔
سند بن علی (864ع۔ تاریخ وفات)
اس نے ان تمام دھاتوں کے نمونے فراہم کئے جو اس کے زمانے تک دریافت ہوچکی تھیں۔ پھر پانی کو معیار مقرر کرکے اس نے نہایت صحیح طریقے سے ہر دھات کی متعلق یہ معلوم کیا کہ وہ پانی سے کتنے گنا بھاری ہے۔ ہم آج کی اسطلاح میں اس نسبت کو جو کسی شئے کے وزن اور اسکے مساوی الحجم پانی کے وزن میں پائی جاتی ہے، اس شئے کی کثافت اضافی یا وزن مخصوص (Specific Gravity/Relative Density) کہتے ہیں۔ اس نسبت کے ذریعے ہم یہ اندازہ لگانے میں کامیاب ہوتے ہیں کہ کوئی چیز پانی کے مقابلے میں کتنا گنا بھاری ہے۔
علی بن عیسیٰ اصطرلابی :
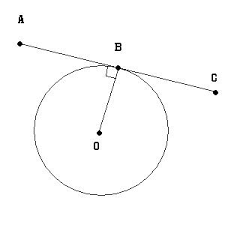
وہ ہئیت کے آلات، بالخصوص اصطرلاب بنانے میں غیر معمولی مہارت رکھتا تھا اور اس وجہ سے "اصطرلابی" مشہور تھا۔ اصطرلاب جسکو انگریزی میں (Astrolabe ) کہاجاتا ہے، دراصل ارسطویا ابرخس یونانی کاایجادکردہ،پیتلکا ایک مدورقرص نماقدیمآلہ تھا جس کےخطوطاورنشاناتکے ذریعےاجرام فلکیکی بلندیاں معلوم کی جاتی تھیں۔ گو اس ایجاد کاسہرا یونانیوں کے سر ہے، لیکن اس کو ترقی دینا اور جدید شکل دینے کی کاوش مسلم سائنسدانوں کے سر کی جاتی ہے۔ اصطرلاب کی سب سے ترقی یافتہ"سدس" کہلاتی تھی۔ اسکی درجہ بردار قوس جس پر زاوئیے کے درجے لگے ہوتے تھے، ایک دائرے کے چھٹے حصے کے برابر ہوتی تھی اور اسی وجہ سے اسکا نام "سدس" تھا، کیونکہ سدس کے لفظی معنی "چھٹے حصے" کے ہیں۔ لاطینی زبان میں ترجمہ کرنے والوں نے اس "سدس" کو سیکسٹنٹ (Sextant) بنالیا جو آج کل اس آلے کا مروجہ نام ہے اور جسکے لفظی معنی لاطینی میں وہی ہیں جو عربی میں سدس کے ہیں۔
حبس جاصب (830 ع سن وفات)
علم المثلٹ (Trigonometry ) اسکی تحقیقات کا خاص میدان تھا، چنانچہ زاوئیے کی مشہور نسبتوں میں سے اس نے فضل جیوب (Cotangent, Cotθ) اور قاطع (secant, secθکو پہلی مرتبہ ٹرگنومیڑی میں رواج دیا تھا اور اسکے نقشے (Tables) تیار کئے تھے۔
نامور مسلم سائنسدان
کتاب : پروفیسر حمید عسکری۔ (مجلس ترقی ادب)
جابر بن حیان (786 ع)
وہ کیمیا کے تمام تجرباتی عملوں مثلا حل کرنا (Dissolve) ، فلٹر کرنا (Filtrate) کشید کرنا (Distillation ) عمل تصعید (Sublimation (اشیاء کا جوہر اڑانا اور قلماؤ (Crystallization) کے ذریعےاشیاء کی قلمیں بنانا، اس سب سے وہ واقف تھا، بلکہ اپنے کیمیائی تجربوں میں ان سے بکثرت کام بھی لیتا تھا۔ اس نے اپنی کیمیا کی کتابوں میں فولاد بنانے، چمڑے کو رنگنے، دھاتوں کو مصفی کرنے (Metallurgy) موم جامہ بنانے، لوہےکو زنگ سے بچانے کےک لئے اس پر وارنش کرنے، بالوں کو سیاہ کرنے کے لئے خضاب تیار کرنے اور اس قسم کی بیسوں مفید اشیاء بنانے کے طریقے بیان کیئے ہیں۔
سند بن علی (864ع۔ تاریخ وفات)
اس نے ان تمام دھاتوں کے نمونے فراہم کئے جو اس کے زمانے تک دریافت ہوچکی تھیں۔ پھر پانی کو معیار مقرر کرکے اس نے نہایت صحیح طریقے سے ہر دھات کی متعلق یہ معلوم کیا کہ وہ پانی سے کتنے گنا بھاری ہے۔ ہم آج کی اسطلاح میں اس نسبت کو جو کسی شئے کے وزن اور اسکے مساوی الحجم پانی کے وزن میں پائی جاتی ہے، اس شئے کی کثافت اضافی یا وزن مخصوص (Specific Gravity/Relative Density) کہتے ہیں۔ اس نسبت کے ذریعے ہم یہ اندازہ لگانے میں کامیاب ہوتے ہیں کہ کوئی چیز پانی کے مقابلے میں کتنا گنا بھاری ہے۔
علی بن عیسیٰ اصطرلابی :
وہ ہئیت کے آلات، بالخصوص اصطرلاب بنانے میں غیر معمولی مہارت رکھتا تھا اور اس وجہ سے "اصطرلابی" مشہور تھا۔ اصطرلاب جسکو انگریزی میں (Astrolabe ) کہاجاتا ہے، دراصل ارسطویا ابرخس یونانی کاایجادکردہ،پیتلکا ایک مدورقرص نماقدیمآلہ تھا جس کےخطوطاورنشاناتکے ذریعےاجرام فلکیکی بلندیاں معلوم کی جاتی تھیں۔ گو اس ایجاد کاسہرا یونانیوں کے سر ہے، لیکن اس کو ترقی دینا اور جدید شکل دینے کی کاوش مسلم سائنسدانوں کے سر کی جاتی ہے۔ اصطرلاب کی سب سے ترقی یافتہ"سدس" کہلاتی تھی۔ اسکی درجہ بردار قوس جس پر زاوئیے کے درجے لگے ہوتے تھے، ایک دائرے کے چھٹے حصے کے برابر ہوتی تھی اور اسی وجہ سے اسکا نام "سدس" تھا، کیونکہ سدس کے لفظی معنی "چھٹے حصے" کے ہیں۔ لاطینی زبان میں ترجمہ کرنے والوں نے اس "سدس" کو سیکسٹنٹ (Sextant) بنالیا جو آج کل اس آلے کا مروجہ نام ہے اور جسکے لفظی معنی لاطینی میں وہی ہیں جو عربی میں سدس کے ہیں۔
حبس جاصب (830 ع سن وفات)
علم المثلٹ (Trigonometry ) اسکی تحقیقات کا خاص میدان تھا، چنانچہ زاوئیے کی مشہور نسبتوں میں سے اس نے فضل جیوب (Cotangent, Cotθ) اور قاطع (secant, secθکو پہلی مرتبہ ٹرگنومیڑی میں رواج دیا تھا اور اسکے نقشے (Tables) تیار کئے تھے۔